Leetcode
Data Structures & Algorithms
➤ 115. Distinct Subsequences
Problem:
Given a string S and a string T, count the number of distinct subsequences of S which equals T.
A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, "ACE" is a subsequence of "ABCDE" while "AEC" is not).
Example 1:
Input: S = "rabbbit", T = "rabbit"
Output: 3
Explanation:
As shown below, there are 3 ways you can generate "rabbit" from S.
(The caret symbol ^ means the chosen letters)
rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^
Example 2:
Input: S = "babgbag", T = "bag"
Output: 5
Explanation:
As shown below, there are 5 ways you can generate "bag" from S.
(The caret symbol ^ means the chosen letters)
babgbag
^^ ^
babgbag
^^ ^
babgbag
^ ^^
babgbag
^ ^^
babgbag
^^^
Solution:
Define f(i, j) to be the number of ways that generate T[0...j) from S[0...i).
For f(i, j) you can always skip S[i-1], but can only take it when S[i-1] === T[j-1].
f(0, j) = 0, j > 0 // nothing to delete
f(i, 0) = 1 // delete all
f(i, j) = f(i-1, j) + (S[i-1] === T[j-1] ? f(i-1, j-1) : 0)
Dynamic array can be used.
/**
* @param {string} s
* @param {string} t
* @return {number}
*/
let numDistinct = function (s, t) {
const lens = s.length;
const lent = t.length;
const dp = new Array(lent + 1).fill(0);
dp[0] = 1;
for (let i = 1; i <= lens; i++) {
for (let j = lent; j >= 1; j--) {
if (s[i - 1] === t[j - 1]) {
dp[j] += dp[j - 1];
}
}
}
return dp[lent];
};
Difficulty: Medium Related Topics: "Tree": https://leetcode.com/tag/tree "Depth-first Search": https://leetcode.com/tag/depth-first-search Similar Questions: "Populating Next Right Pointers in Each Node II": https://leetcode.com/problems/populating-next-right-pointers-in-each-node-ii "Binary Tree Right Side View": https://leetcode.com/problems/binary-tree-right-side-view
➤ 116. Populating Next Right Pointers in Each Node
Problem:
Given a binary tree
struct TreeLinkNode {
TreeLinkNode *left;
TreeLinkNode *right;
TreeLinkNode *next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Note:
- You may only use constant extra space.
- Recursive approach is fine, implicit stack space does not count as extra space for this problem.
- You may assume that it is a perfect binary tree (ie, all leaves are at the same level, and every parent has two children).
Example:
Given the following perfect binary tree,
1
/ \
2 3
/ \ / \
4 5 6 7
After calling your function, the tree should look like:
1 -> NULL
/ \
2 -> 3 -> NULL
/ \ / \
4->5->6->7 -> NULL
Solution:
ONE
Recursive.
For every node:
- Left child: points to
node.right. - Right child: points to
node.next.leftifnode.nextexists.
/**
* Definition for binary tree with next pointer.
* function TreeLinkNode(val) {
* this.val = val;
* this.left = this.right = this.next = null;
* }
*/
/**
* @param {TreeLinkNode} root
* @return {void} Do not return anything, modify tree in-place instead.
*/
let connect = function (root) {
if (!root) {
return;
}
if (root.left !== null) {
root.left.next = root.right;
connect(root.left);
}
if (root.right !== null) {
if (root.next !== null) {
root.right.next = root.next.left;
}
connect(root.right);
}
};
TWO
Level order traversal.
/**
* Definition for binary tree with next pointer.
* function TreeLinkNode(val) {
* this.val = val;
* this.left = this.right = this.next = null;
* }
*/
/**
* @param {TreeLinkNode} root
* @return {void} Do not return anything, modify tree in-place instead.
*/
let connect = function (root) {
if (!root) {
return;
}
const queue = [NaN, root];
while (queue.length > 1) {
const node = queue.shift();
if (node !== node) {
for (let i = 0; i < queue.length; i++) {
queue[i].next = queue[i + 1] || null;
}
queue.push(NaN);
} else {
if (node.left !== null) {
queue.push(node.left);
}
if (node.right !== null) {
queue.push(node.right);
}
}
}
};
Difficulty: Medium Related Topics: "Tree": https://leetcode.com/tag/tree "Depth-first Search": https://leetcode.com/tag/depth-first-search Similar Questions: "Populating Next Right Pointers in Each Node": https://leetcode.com/problems/populating-next-right-pointers-in-each-node
➤ 117. Populating Next Right Pointers in Each Node II
Problem:
Given a binary tree
struct TreeLinkNode {
TreeLinkNode *left;
TreeLinkNode *right;
TreeLinkNode *next;
}
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Note:
- You may only use constant extra space.
- Recursive approach is fine, implicit stack space does not count as extra space for this problem.
Example:
Given the following binary tree,
1
/ \
2 3
/ \ \
4 5 7
After calling your function, the tree should look like:
1 -> NULL
/ \
2 -> 3 -> NULL
/ \ \
4-> 5 -> 7 -> NULL
Solution:
ONE
Recursive. See 116. Populating Next Right Pointers in Each Node.
The tree may not be perfect now. So keep finding next until there is a node with children, or null.
This also means post-order traversal is required.
/**
* Definition for binary tree with next pointer.
* function TreeLinkNode(val) {
* this.val = val;
* this.left = this.right = this.next = null;
* }
*/
/**
* @param {TreeLinkNode} root
* @return {void} Do not return anything, modify tree in-place instead.
*/
let connect = function (root) {
if (!root) {
return;
}
let next = null;
for (let node = root.next; node !== null; node = node.next) {
if (node.left !== null) {
next = node.left;
break;
}
if (node.right !== null) {
next = node.right;
break;
}
}
if (root.right !== null) {
root.right.next = next;
}
if (root.left !== null) {
root.left.next = root.right || next;
}
connect(root.right);
connect(root.left);
};
TWO
Level order traversal. Exact same as 116. Populating Next Right Pointers in Each Node.
/**
* Definition for binary tree with next pointer.
* function TreeLinkNode(val) {
* this.val = val;
* this.left = this.right = this.next = null;
* }
*/
/**
* @param {TreeLinkNode} root
* @return {void} Do not return anything, modify tree in-place instead.
*/
let connect = function (root) {
if (!root) {
return;
}
const queue = [NaN, root];
while (queue.length > 1) {
const node = queue.shift();
if (node !== node) {
for (let i = 0; i < queue.length; i++) {
queue[i].next = queue[i + 1] || null;
}
queue.push(NaN);
} else {
if (node.left !== null) {
queue.push(node.left);
}
if (node.right !== null) {
queue.push(node.right);
}
}
}
};
Difficulty: Easy Related Topics: "Array": https://leetcode.com/tag/array Similar Questions: "Pascal's Triangle II": https://leetcode.com/problems/pascals-triangle-ii
➤ 118. Pascal's Triangle
Problem:
Given a non-negative integer numRows, generate the first numRows of Pascal's triangle.

In Pascal's triangle, each number is the sum of the two numbers directly above it.
Example:
Input: 5
Output:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
Solution:
Dynamic Programming 101.
/**
* @param {number} numRows
* @return {number[][]}
*/
let generate = function (numRows) {
if (numRows <= 0) {
return [];
}
const result = [[1]];
for (let i = 1; i < numRows; i++) {
const lastRow = result[i - 1];
const row = [1];
for (let j = 1; j < i; j++) {
row[j] = lastRow[j] + lastRow[j - 1];
}
row.push(1);
result.push(row);
}
return result;
};
Difficulty: Easy Related Topics: "Array": https://leetcode.com/tag/array Similar Questions: "Pascal's Triangle": https://leetcode.com/problems/pascals-triangle
➤ 119. Pascal's Triangle II
Problem:
Given a non-negative index k where k ≤ 33, return the kth index row of the Pascal's triangle.
Note that the row index starts from 0.

In Pascal's triangle, each number is the sum of the two numbers directly above it.
Example:
Input: 3
Output: [1,3,3,1]
Follow up:
Could you optimize your algorithm to use only O(k) extra space?
Solution:
Dynamic Programming 101 with dynamic array.
State (i, j) depends on (i-1, j) and (i-1, j-1). So to access (i-1, j-1) iteration must be from right to left.
/**
* @param {number} rowIndex
* @return {number[]}
*/
let getRow = function (rowIndex) {
if (rowIndex < 0) {
return [];
}
const row = [1];
for (let i = 1; i <= rowIndex; i++) {
for (let j = i - 1; j > 0; j--) {
row[j] += row[j - 1];
}
row.push(1);
}
return row;
};
Difficulty: Medium Related Topics: "Array": https://leetcode.com/tag/array "Dynamic Programming": https://leetcode.com/tag/dynamic-programming
➤ 120. Triangle
Problem:
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
Note:
Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.
Solution:
Define f(i, j) to be the minimum path sum from triangle[0][0] to triangle[i][j].
f(i, 0) = f(i-1, j) + triangle[i][0]
f(i, j) = min( f(i-1, j-1), f(i-1, j) ) + triangle[i][j], 0 < j < i
f(i, i) = f(i-1, i-1) + triangle[i][i], i > 0
Dynamic array can be used.
/**
* @param {number[][]} triangle
* @return {number}
*/
let minimumTotal = function (triangle) {
if (triangle.length <= 0) {
return 0;
}
const dp = [triangle[0][0]];
for (let i = 1; i < triangle.length; i++) {
dp[i] = dp[i - 1] + triangle[i][i];
for (let j = i - 1; j >= 1; j--) {
dp[j] = Math.min(dp[j], dp[j - 1]) + triangle[i][j];
}
dp[0] += triangle[i][0];
}
return Math.min(...dp);
};
Difficulty: Easy Related Topics: "Array": https://leetcode.com/tag/array "Dynamic Programming": https://leetcode.com/tag/dynamic-programming Similar Questions: "Maximum Subarray": https://leetcode.com/problems/maximum-subarray "Best Time to Buy and Sell Stock II": https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii "Best Time to Buy and Sell Stock III": https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii "Best Time to Buy and Sell Stock IV": https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv "Best Time to Buy and Sell Stock with Cooldown": https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-cooldown
➤ 121. Best Time to Buy and Sell Stock
Problem:
Say you have an array for which the ith element is the price of a given stock on day i.
If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.
Note that you cannot sell a stock before you buy one.
Example 1:
Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Not 7-1 = 6, as selling price needs to be larger than buying price.
Example 2:
Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.
Solution:
Only care about positive profits. Take the frist item as base and scan to the right. If we encounter an item j whose price price[j] is lower than the base (which means if we sell now the profit would be negative), we sell j-1 instead and make j the new base.
Because price[j] is lower that the base, using j as new base is guaranteed to gain more profit comparing to the old one.
/**
* @param {number[]} prices
* @return {number}
*/
let maxProfit = function (prices) {
let max = 0;
let base = prices[0];
for (let i = 1; i < prices.length; i++) {
const profit = prices[i] - base;
if (profit > max) {
max = profit;
} else if (profit < 0) {
base = prices[i];
}
}
return max;
};
Difficulty: Easy Related Topics: "Array": https://leetcode.com/tag/array "Greedy": https://leetcode.com/tag/greedy Similar Questions: "Best Time to Buy and Sell Stock": https://leetcode.com/problems/best-time-to-buy-and-sell-stock "Best Time to Buy and Sell Stock III": https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii "Best Time to Buy and Sell Stock IV": https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv "Best Time to Buy and Sell Stock with Cooldown": https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-cooldown "Best Time to Buy and Sell Stock with Transaction Fee": https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee
➤ 122. Best Time to Buy and Sell Stock II
Problem:
Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times).
Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).
Example 1:
Input: [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Example 2:
Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
engaging multiple transactions at the same time. You must sell before buying again.
Example 3:
Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.
Solution:
Sell immediately after the price drops. Or in other perspective, it is the sum of all the incremental pairs (buy in then immediately sell out).
/**
* @param {number[]} prices
* @return {number}
*/
let maxProfit = function (prices) {
let max = 0;
for (let i = 1; i < prices.length; i++) {
if (prices[i] > prices[i - 1]) {
max += prices[i] - prices[i - 1];
}
}
return max;
};
Difficulty: Hard Related Topics: "Array": https://leetcode.com/tag/array "Dynamic Programming": https://leetcode.com/tag/dynamic-programming Similar Questions: "Best Time to Buy and Sell Stock": https://leetcode.com/problems/best-time-to-buy-and-sell-stock "Best Time to Buy and Sell Stock II": https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii "Best Time to Buy and Sell Stock IV": https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv "Maximum Sum of 3 Non-Overlapping Subarrays": https://leetcode.com/problems/maximum-sum-of-3-non-overlapping-subarrays
➤ 123. Best Time to Buy and Sell Stock III
Problem:
Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete at most two transactions.
**Note:**You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).
Example 1:
Input: [3,3,5,0,0,3,1,4]
Output: 6
Explanation: Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.
Example 2:
Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
engaging multiple transactions at the same time. You must sell before buying again.
Example 3:
Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.
Solution:
Multiple transactions may not be engaged in at the same time. That means if we view the days that involed in the same transaction as a group, there won't be any intersection. We may complete at most two transactions, so divide the days into two groups, [0...k] and [k...n-1]. Notice k exists in both groups because technically we can sell out then immediately buy in at the same day.
Define p1(i) to be the max profit of day [0...i]. This is just like the problem of 121. Best Time to Buy and Sell Stock.
p1(0) = 0
p1(i) = max( p1(i-1), prices[i] - min(prices[0], ..., prices[i-1]) ), 0 < i <= n-1
Define p2(i) to be the max profit of day [i...n-1]. This is the mirror of p1.
p2(n-1) = 0
p2(i) = max( p2(i+1), max(prices[i], ..., prices[n-1]) - prices[i] ), n-1 > i >= 0
Define f(k) to be p1(k) + p2(k). We need to get max( f(0), ..., f(n-1) ).
/**
* @param {number[]} prices
* @return {number}
*/
let maxProfit = function (prices) {
const len = prices.length;
if (len <= 1) {
return 0;
}
const dp = [0];
let min = prices[0];
for (let i = 1; i < len; i++) {
dp[i] = Math.max(dp[i - 1], prices[i] - min);
min = Math.min(prices[i], min);
}
let p2 = 0;
let max = prices[len - 1];
for (let i = len - 2; i >= 0; i--) {
max = Math.max(prices[i], max);
p2 = Math.max(p2, max - prices[i]);
dp[i] += p2;
}
return Math.max(...dp);
};
Difficulty: Hard Related Topics: "Tree": https://leetcode.com/tag/tree "Depth-first Search": https://leetcode.com/tag/depth-first-search Similar Questions: "Path Sum": https://leetcode.com/problems/path-sum "Sum Root to Leaf Numbers": https://leetcode.com/problems/sum-root-to-leaf-numbers "Path Sum IV": https://leetcode.com/problems/path-sum-iv "Longest Univalue Path": https://leetcode.com/problems/longest-univalue-path
➤ 124. Binary Tree Maximum Path Sum
Problem:
Given a non-empty binary tree, find the maximum path sum.
For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.
Example 1:
Input: [1,2,3]
1
/ \
2 3
Output: 6
Example 2:
Input: [-10,9,20,null,null,15,7]
-10
/ \
9 20
/ \
15 7
Output: 42
Solution:
For every node, there are six possible ways to get the max path sum:
With
node.valnode.valplus the max sum of a path that ends withnode.left.node.valplus the max sum of a path that starts withnode.right.node.valplus the max sum of both paths.- Just
node.val(the max sum of both paths are negative).
Without
node.val(disconnected)- The max-sum path is somewhere under the
node.leftsubtree. - The max-sum path is somewhere under the
node.rightsubtree.
- The max-sum path is somewhere under the
There are two ways to implement this.
ONE
Define a function that returns two values. The max sum of a path that may or may not end with root node, and the max sum of the path that ends with root node.
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
let maxPathSum = function (root) {
return Math.max(..._maxPathSum(root));
};
/**
* @param {TreeNode} root
* @return {number[]}
*/
function _maxPathSum(root) {
if (!root) {
return [-Infinity, -Infinity];
}
const left = _maxPathSum(root.left);
const right = _maxPathSum(root.right);
return [Math.max(left[0], right[0], root.val + Math.max(0, left[1], right[1], left[1] + right[1])), Math.max(left[1], right[1], 0) + root.val];
}
TWO
Just return the later (max sum of a path that ends with root). Maintain a global variable to store the disconnected max sum.
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
let maxPathSum = function (root) {
const global = { max: -Infinity };
_maxPathSum(root, global);
return global.max;
};
/**
* @param {TreeNode} root
* @param {object} global
* @param {number} global.max
* @return {number[]}
*/
function _maxPathSum(root, global) {
if (!root) {
return -Infinity;
}
const left = _maxPathSum(root.left, global);
const right = _maxPathSum(root.right, global);
const localMax = Math.max(left, right, 0) + root.val;
global.max = Math.max(global.max, localMax, root.val + left + right);
return localMax;
}
Difficulty: Easy Related Topics: "Two Pointers": https://leetcode.com/tag/two-pointers "String": https://leetcode.com/tag/string Similar Questions: "Palindrome Linked List": https://leetcode.com/problems/palindrome-linked-list "Valid Palindrome II": https://leetcode.com/problems/valid-palindrome-ii
➤ 125. Valid Palindrome
Problem:
Given a string, determine if it is a palindrome, considering only alphanumeric characters and ignoring cases.
Note: For the purpose of this problem, we define empty string as valid palindrome.
Example 1:
Input: "A man, a plan, a canal: Panama"
Output: true
Example 2:
Input: "race a car"
Output: false
Solution:
ONE
/**
* @param {string} s
* @return {boolean}
*/
let isPalindrome = function (s) {
const clean = s.toLowerCase().split(/[^a-z0-9]*/);
return clean.join('') === clean.reverse().join('');
};
TWO
Remove non-alphanumeric characters then compare.
/**
* @param {string} s
* @return {boolean}
*/
let isPalindrome = function (s) {
const clean = s.replace(/[^a-zA-Z0-9]/g, '').toLowerCase();
for (let i = 0, j = clean.length - 1; i < j; i++, j--) {
if (clean[i] !== clean[j]) {
return false;
}
}
return true;
};
THREE
Compare the char codes.
/**
* @param {string} s
* @return {boolean}
*/
let isPalindrome = function (s) {
for (let i = 0, j = s.length - 1; i < j; i++, j--) {
let left = s.charCodeAt(i);
while (i < j && (left < 48 || (left > 57 && left < 65) || (left > 90 && left < 97) || left > 122)) {
left = s.charCodeAt(++i);
}
if (i >= j) {
return true;
}
if (left >= 65 && left <= 90) {
left += 32;
}
let right = s.charCodeAt(j);
while (i < j && (right < 48 || (right > 57 && right < 65) || (right > 90 && right < 97) || right > 122)) {
right = s.charCodeAt(--j);
}
if (i >= j) {
return true;
}
if (right >= 65 && right <= 90) {
right += 32;
}
if (left !== right) {
return false;
}
}
return true;
};
Difficulty: Hard Related Topics: "Array": https://leetcode.com/tag/array "String": https://leetcode.com/tag/string "Backtracking": https://leetcode.com/tag/backtracking "Breadth-first Search": https://leetcode.com/tag/breadth-first-search Similar Questions: "Word Ladder": https://leetcode.com/problems/word-ladder
➤ 126. Word Ladder II
Problem:
Given two words (beginWord and endWord), and a dictionary's word list, find all shortest transformation sequence(s) from beginWord to endWord, such that:
- Only one letter can be changed at a time
- Each transformed word must exist in the word list. Note that beginWord is not a transformed word.
Note:
- Return an empty list if there is no such transformation sequence.
- All words have the same length.
- All words contain only lowercase alphabetic characters.
- You may assume no duplicates in the word list.
- You may assume beginWord and endWord are non-empty and are not the same.
Example 1:
Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]
Output:
[
["hit","hot","dot","dog","cog"],
["hit","hot","lot","log","cog"]
]
Example 2:
Input:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]
Output: []
Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.
Solution:
This is just like 127. Word Ladder.
The constrain still works, but instead of deleting the words right away, collect them and delete them all when a level ends, so that we can reuse the words (matching different parents in the same level).
The items in the queue are not just words now. Parent nodes are also kept so that we can backtrack the path from the end.
/**
* @param {string} beginWord
* @param {string} endWord
* @param {string[]} wordList
* @return {string[][]}
*/
function findLadders(beginWord, endWord, wordList) {
wordList = new Set(wordList);
if (!wordList.has(endWord)) {
return [];
}
const ALPHABET = 'abcdefghijklmnopqrstuvwxyz';
const result = [];
let isEndWordFound = false;
const levelWords = new Set();
const queue = [[beginWord, null], null];
while (queue.length > 1) {
const node = queue.shift();
if (node === null) {
if (isEndWordFound) {
break;
}
levelWords.forEach((word) => wordList.delete(word));
levelWords.clear();
queue.push(null);
continue;
}
const word = node[0];
for (let i = word.length - 1; i >= 0; i--) {
const head = word.slice(0, i);
const tail = word.slice(i + 1);
for (let c = 0; c < 26; c++) {
if (ALPHABET[c] !== word[i]) {
const w = head + ALPHABET[c] + tail;
if (w === endWord) {
const path = [endWord];
for (let n = node; n !== null; n = n[1]) {
path.unshift(n[0]);
}
result.push(path);
isEndWordFound = true;
}
if (wordList.has(w)) {
levelWords.add(w);
queue.push([w, node]);
}
}
}
}
}
return result;
}
Difficulty: Medium Related Topics: "Breadth-first Search": https://leetcode.com/tag/breadth-first-search Similar Questions: "Word Ladder II": https://leetcode.com/problems/word-ladder-ii "Minimum Genetic Mutation": https://leetcode.com/problems/minimum-genetic-mutation
➤ 127. Word Ladder
Problem:
Given two words (beginWord and endWord), and a dictionary's word list, find the length of shortest transformation sequence from beginWord to endWord, such that:
- Only one letter can be changed at a time.
- Each transformed word must exist in the word list. Note that beginWord is not a transformed word.
Note:
- Return 0 if there is no such transformation sequence.
- All words have the same length.
- All words contain only lowercase alphabetic characters.
- You may assume no duplicates in the word list.
- You may assume beginWord and endWord are non-empty and are not the same.
Example 1:
Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]
Output: 5
Explanation: As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog",
return its length 5.
Example 2:
Input:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]
Output: 0
Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.
Solution:
Think of it as building a tree, with begineWord as root and endWord as leaves.
The best way control the depth (length of the shortest transformations) while building the tree is level-order traversal (BFS).
We do not actually build the tree because it is expensive (astronomical if the list is huge). In fact, we only need one shortest path. So just like Dijkstra's algorithm, we say that the first time (level i) we encounter a word that turns out to be in a shortest path, then level i is the lowest level this word could ever get. We can safely remove it from the wordList.
To find all the next words, instead of filtering the wordList, enumerate all 25 possible words and check if in wordList.
/**
* @param {string} beginWord
* @param {string} endWord
* @param {string[]} wordList
* @return {number}
*/
let ladderLength = function (beginWord, endWord, wordList) {
wordList = new Set(wordList);
if (!wordList.has(endWord)) {
return 0;
}
const ALPHABET = 'abcdefghijklmnopqrstuvwxyz';
let level = 1;
const queue = [beginWord, null];
while (queue.length > 1) {
const word = queue.shift();
if (word === null) {
level++;
queue.push(null);
continue;
}
for (let i = word.length - 1; i >= 0; i--) {
const head = word.slice(0, i);
const tail = word.slice(i + 1);
for (let c = 0; c < 26; c++) {
if (ALPHABET[c] !== word[i]) {
const word = head + ALPHABET[c] + tail;
if (word === endWord) {
return level + 1;
}
if (wordList.delete(word)) {
queue.push(word);
}
}
}
}
}
return 0;
};
Difficulty: Hard Related Topics: "Array": https://leetcode.com/tag/array "Union Find": https://leetcode.com/tag/union-find Similar Questions: "Binary Tree Longest Consecutive Sequence": https://leetcode.com/problems/binary-tree-longest-consecutive-sequence
➤ 128. Longest Consecutive Sequence
Problem:
Given an unsorted array of integers, find the length of the longest consecutive elements sequence.
Your algorithm should run in O(n) complexity.
Example:
Input: [100, 4, 200, 1, 3, 2]
Output: 4
Explanation: The longest consecutive elements sequence is [1, 2, 3, 4]. Therefore its length is 4.
Solution:
Build a Set from the list. Pick a number, find all it's adjacent numbers that are also in the Set. Count them and remove them all from the Set. Repeat until the Set is empty. Time complexity O(n + n) = O(n).
/**
* @param {number[]} nums
* @return {number}
*/
let longestConsecutive = function (nums) {
const numSet = new Set(nums);
let maxCount = 0;
while (numSet.size > 0) {
const num = numSet.values().next().value;
numSet.delete(num);
let count = 1;
for (let n = num + 1; numSet.delete(n); n++) {
count++;
}
for (let n = num - 1; numSet.delete(n); n--) {
count++;
}
if (count > maxCount) {
maxCount = count;
}
}
return maxCount;
};
Difficulty: Medium Related Topics: "Tree": https://leetcode.com/tag/tree "Depth-first Search": https://leetcode.com/tag/depth-first-search Similar Questions: "Path Sum": https://leetcode.com/problems/path-sum "Binary Tree Maximum Path Sum": https://leetcode.com/problems/binary-tree-maximum-path-sum
➤ 129. Sum Root to Leaf Numbers
Problem:
Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number.
An example is the root-to-leaf path 1->2->3 which represents the number 123.
Find the total sum of all root-to-leaf numbers.
Note: A leaf is a node with no children.
Example:
Input: [1,2,3]
1
/ \
2 3
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.
Example 2:
Input: [4,9,0,5,1]
4
/ \
9 0
/ \
5 1
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.
Solution:
To write a clean solution for this promblem, use 0 as indicator of leaf node. If all the children get 0, it is a leaf node, return the sum of current level.
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
let sumNumbers = function (root, sum = 0) {
if (!root) {
return 0;
}
sum = sum * 10 + root.val;
return sumNumbers(root.left, sum) + sumNumbers(root.right, sum) || sum;
};
Difficulty: Medium Related Topics: "Depth-first Search": https://leetcode.com/tag/depth-first-search "Breadth-first Search": https://leetcode.com/tag/breadth-first-search "Union Find": https://leetcode.com/tag/union-find Similar Questions: "Number of Islands": https://leetcode.com/problems/number-of-islands "Walls and Gates": https://leetcode.com/problems/walls-and-gates
➤ 130. Surrounded Regions
Problem:
Given a 2D board containing 'X' and 'O' (the letter O), capture all regions surrounded by 'X'.
A region is captured by flipping all 'O's into 'X's in that surrounded region.
Example:
X X X X
X O O X
X X O X
X O X X
After running your function, the board should be:
X X X X
X X X X
X X X X
X O X X
Explanation:
Surrounded regions shouldn't be on the border, which means that any 'O' on the border of the board are not flipped to 'X'. Any 'O' that is not on the border and it is not connected to an 'O' on the border will be flipped to 'X'. Two cells are connected if they are adjacent cells connected horizontally or vertically.
Solution:
Find all the Os that are connected to the Os on the border, change them to #. Then scan the board, change O to X and # back to O.
The process of finding the connected Os is just like tree traversal. Os on the border are the same level. Their children are the second level. And so on.
So both BFS and DFS are good. I prefer BFS when pruning is not needed in favor of its readability.
/**
* @param {character[][]} board
* @return {void} Do not return anything, modify board in-place instead.
*/
let solve = function (board) {
const height = board.length;
if (height <= 1) {
return;
}
const width = board[0].length;
if (width <= 1) {
return;
}
const rowend = height - 1;
const colend = width - 1;
const queue = [];
for (let row = 0; row < height; row++) {
if (board[row][0] === 'O') {
board[row][0] = '#';
queue.push(row, 0);
}
if (board[row][colend] === 'O') {
board[row][colend] = '#';
queue.push(row, colend);
}
}
for (let col = 0; col < width; col++) {
if (board[0][col] === 'O') {
board[0][col] = '#';
queue.push(0, col);
}
if (board[rowend][col] === 'O') {
board[rowend][col] = '#';
queue.push(rowend, col);
}
}
while (queue.length > 0) {
const row = queue.shift();
const col = queue.shift();
if (row < rowend && board[row + 1][col] === 'O') {
board[row + 1][col] = '#';
queue.push(row + 1, col);
}
if (row > 0 && board[row - 1][col] === 'O') {
board[row - 1][col] = '#';
queue.push(row - 1, col);
}
if (board[row][col + 1] === 'O') {
board[row][col + 1] = '#';
queue.push(row, col + 1);
}
if (board[row][col - 1] === 'O') {
board[row][col - 1] = '#';
queue.push(row, col - 1);
}
}
for (let row = 0; row < height; row++) {
for (let col = 0; col < width; col++) {
if (board[row][col] === '#') {
board[row][col] = 'O';
} else if (board[row][col] === 'O') {
board[row][col] = 'X';
}
}
}
};
Difficulty: Medium Related Topics: "Depth-first Search": https://leetcode.com/tag/depth-first-search "Breadth-first Search": https://leetcode.com/tag/breadth-first-search "Graph": https://leetcode.com/tag/graph Similar Questions: "Copy List with Random Pointer": https://leetcode.com/problems/copy-list-with-random-pointer
➤ 133. Clone Graph
Problem:
Given the head of a graph, return a deep copy (clone) of the graph. Each node in the graph contains a label (int) and a list (List[UndirectedGraphNode]) of its neighbors. There is an edge between the given node and each of the nodes in its neighbors.
OJ's undirected graph serialization (so you can understand error output):
Nodes are labeled uniquely.
We use # as a separator for each node, and , as a separator for node label and each neighbor of the node.
As an example, consider the serialized graph {0,1,2#1,2#2,2}.
The graph has a total of three nodes, and therefore contains three parts as separated by #.
- First node is labeled as
0. Connect node0to both nodes1and2. - Second node is labeled as
1. Connect node1to node2. - Third node is labeled as
2. Connect node2to node2(itself), thus forming a self-cycle.
Visually, the graph looks like the following:
1
/ \
/ \
0 --- 2
/ \
\_/
Note: The information about the tree serialization is only meant so that you can understand error output if you get a wrong answer. You don't need to understand the serialization to solve the problem.
Solution:
DFS. Cache the visited node before entering the next recursion.
/**
* Definition for undirected graph.
* function UndirectedGraphNode(label) {
* this.label = label;
* this.neighbors = []; // Array of UndirectedGraphNode
* }
*/
/**
* @param {UndirectedGraphNode} graph
* @return {UndirectedGraphNode}
*/
let cloneGraph = function (graph) {
const cache = {};
return _clone(graph);
function _clone(graph) {
if (!graph) {
return graph;
}
const label = graph.label;
if (!cache[label]) {
cache[label] = new UndirectedGraphNode(label);
cache[label].neighbors = graph.neighbors.map(_clone);
}
return cache[label];
}
};

/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
const upsideDownBinaryTree = function (root) {
let curr = root;
let next = null;
let temp = null;
let prev = null;
while (curr !== null) {
next = curr.left;
curr.left = temp;
temp = curr.right;
curr.right = prev;
prev = curr;
curr = next;
}
return prev;
};
// another
const upsideDownBinaryTree = function (root) {
if (root == null || root.left == null) {
return root;
}
const newRoot = upsideDownBinaryTree(root.left);
root.left.left = root.right;
root.left.right = root;
root.left = null;
root.right = null;
return newRoot;
};

/**
* @param {number[]} A
* @return {number}
*/
const maxSubarraySumCircular = function (A) {
let minSum = Infinity,
sum = 0,
maxSum = -Infinity,
curMax = 0,
curMin = 0;
for (let a of A) {
sum += a;
curMax = Math.max(curMax + a, a);
maxSum = Math.max(maxSum, curMax);
curMin = Math.min(curMin + a, a);
minSum = Math.min(minSum, curMin);
}
return maxSum > 0 ? Math.max(maxSum, sum - minSum) : maxSum;
};
➤ Balanced Binary Tree - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
Given a binary tree, determine if it is height-balanced.
For this problem, a height-balanced binary tree is defined as:
a binary tree in which the left and right subtrees of every node differ in height by no more than 1.
Example 1:
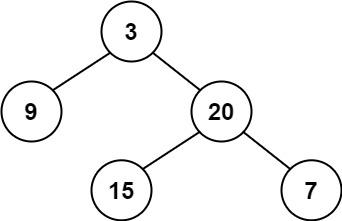
Input: root = [3,9,20,null,null,15,7] Output: true
Example 2:
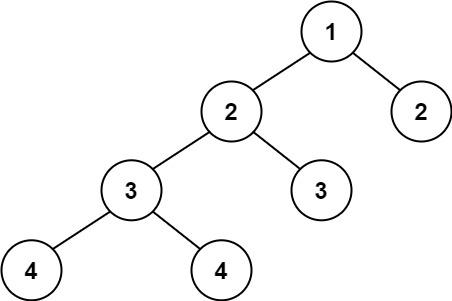
Input: root = [1,2,2,3,3,null,null,4,4] Output: false
Example 3:
Input: root = [] Output: true
Constraints:
- The number of nodes in the tree is in the range
[0, 5000]. -104 <= Node.val <= 104
Source# Convert Sorted Array to Binary Search Tree
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
Given an array where elements are sorted in ascending order, convert it to a height balanced BST.
For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.
Example:
Given the sorted array: [-10,-3,0,5,9],
One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:
0
/ \\
-3 9 / / -10 5
Source# Delete Node in a BST
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.
Basically, the deletion can be divided into two stages:
- Search for a node to remove.
- If the node is found, delete the node.
Follow up: Can you solve it with time complexity O(height of tree)?
Example 1:
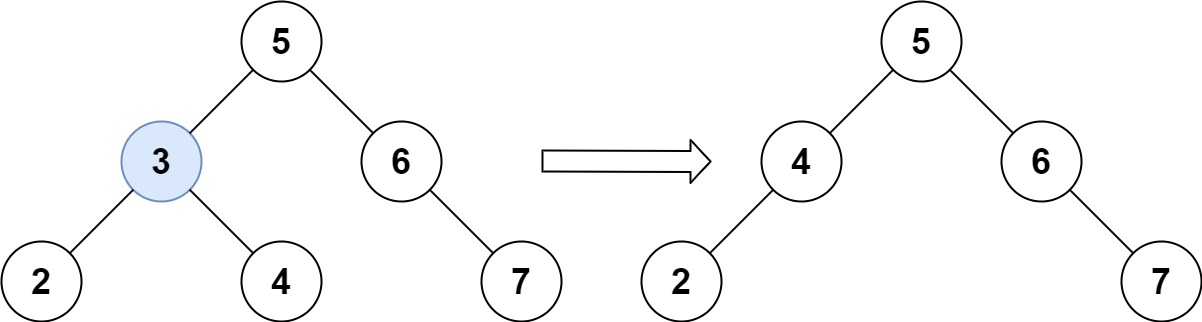
Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.
Example 2:
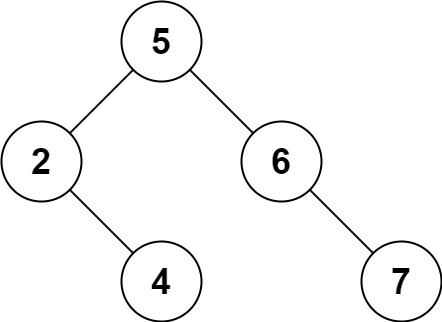
Input: root = [5,3,6,2,4,null,7], key = 0 Output: [5,3,6,2,4,null,7] Explanation: The tree does not contain a node with value = 0.
Example 3:
Input: root = [], key = 0 Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 104]. -105 <= Node.val <= 105- Each node has a unique value.
rootis a valid binary search tree.-105 <= key <= 105
/**
* @param {number[][]} intervals
* @return {number}
*/
const minMeetingRooms = function (intervals) {
const len = intervals.length;
const starts = new Array(len);
const ends = new Array(len);
for (let i = 0; i < len; i++) {
starts[i] = intervals[i][0];
ends[i] = intervals[i][1];
}
starts.sort((a, b) => a - b);
ends.sort((a, b) => a - b);
let rooms = 0;
let endsIdx = 0;
for (let i = 0; i < len; i++) {
if (starts[i] < ends[endsIdx]) rooms++;
else endsIdx++;
}
return rooms;
};



